Quantum diffie hellman key exchange – Quantum Diffie-Hellman Key Exchange: Forget everything you thought you knew about secure communication. This isn’t your grandpappy’s encryption. We’re diving headfirst into the quantum realm, where the very laws of physics are bent to create unbreakable digital locks. Prepare to have your mind blown as we explore how quantum mechanics supercharges the classic Diffie-Hellman key exchange, making it practically impervious to even the most advanced attacks – both classical and quantum.
Imagine a world where your online banking, secret government communications, and even your daily chats are utterly secure. That’s the promise of Quantum Diffie-Hellman. It leverages the mind-bending principles of quantum mechanics to create cryptographic keys with unprecedented security. We’ll unpack the intricacies of Quantum Key Distribution (QKD), explore the quantum algorithms that make it all tick, and delve into the real-world applications that are already emerging. Get ready for a journey into the future of secure communication.
Introduction to Quantum Diffie-Hellman Key Exchange: Quantum Diffie Hellman Key Exchange
Source: medium.com
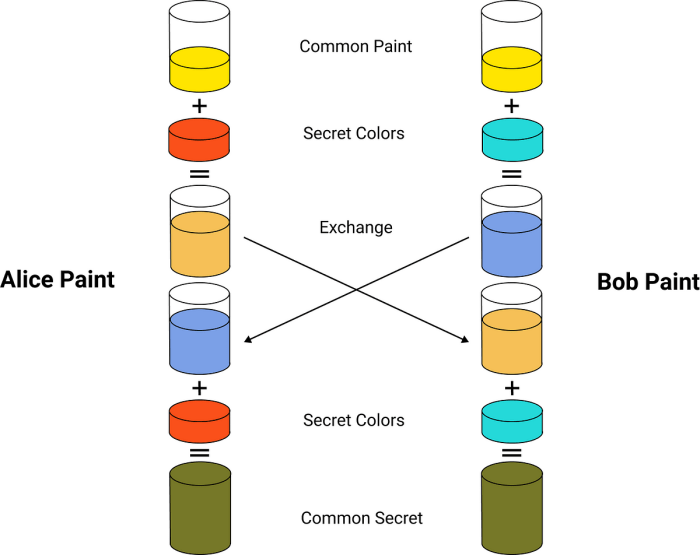
The Diffie-Hellman key exchange, a revolutionary cryptographic breakthrough, allows two parties to establish a shared secret key over an insecure channel. This secret key can then be used for secure communication, even if eavesdroppers intercept the exchanged messages. It’s a cornerstone of modern internet security, powering everything from secure web browsing to online banking. However, the security of classical Diffie-Hellman relies on the computational difficulty of certain mathematical problems, which are vulnerable to attacks from sufficiently powerful quantum computers. This is where the quantum variant steps in, offering a more robust and potentially faster solution.
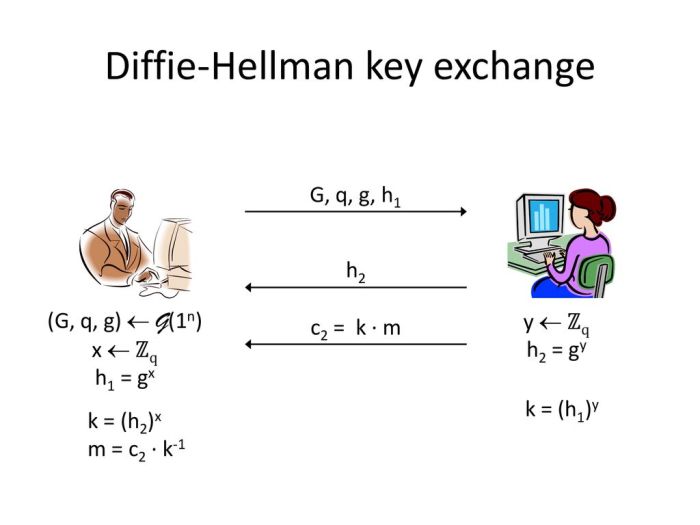
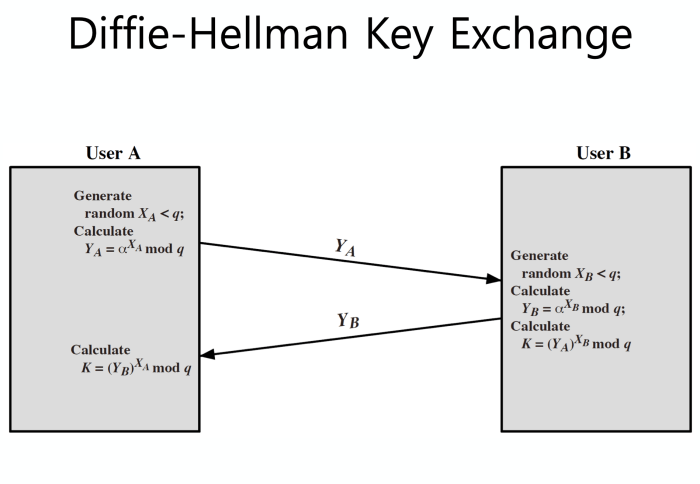
The core principle of Diffie-Hellman involves modular arithmetic and discrete logarithms. Two parties, let’s call them Alice and Bob, publicly agree on two numbers: a prime number, *p*, and a generator, *g*, which is a number whose powers modulo *p* produce all the numbers from 1 to *p-1*. Alice chooses a secret number, *a*, and sends Bob *ga mod p*. Similarly, Bob chooses a secret number, *b*, and sends Alice *gb mod p*. Both Alice and Bob can then calculate the shared secret key: *gab mod p*. An eavesdropper, even if they intercept *ga mod p* and *gb mod p*, cannot easily calculate *gab mod p* without solving the discrete logarithm problem, which is computationally hard for large numbers.
Quantum Enhancements to Diffie-Hellman
Quantum mechanics offers several ways to enhance the Diffie-Hellman key exchange. One promising approach leverages the principles of quantum key distribution (QKD) to generate the initial secret numbers (*a* and *b*) in a way that’s provably secure against quantum attacks. This is because QKD uses the fundamental laws of quantum physics to detect eavesdropping attempts. Furthermore, certain quantum algorithms could potentially accelerate the calculation of the shared secret key, making the process more efficient. While the classical Diffie-Hellman relies on the computational hardness of the discrete logarithm problem, quantum Diffie-Hellman seeks to leverage quantum phenomena to enhance security and speed, mitigating vulnerabilities to future quantum computers.
Classical vs. Quantum Diffie-Hellman
The table below summarizes the key differences between classical and quantum Diffie-Hellman key exchange.
| Feature | Classical Diffie-Hellman | Quantum Diffie-Hellman | Key Difference |
|---|---|---|---|
| Security | Based on the computational hardness of the discrete logarithm problem; vulnerable to attacks from sufficiently powerful quantum computers. | Potentially enhanced security through QKD, making it resistant to quantum attacks. | Quantum resistance and the use of QKD. |
| Speed | Relatively slow for very large keys, limiting practical key sizes. | Potentially faster key generation and exchange due to quantum algorithms. | Quantum speedup potential. |
| Algorithm Complexity | Relies on classical modular arithmetic. | Utilizes quantum mechanics and potentially quantum algorithms. | Underlying algorithmic approach. |
Quantum Key Distribution (QKD) in Quantum Diffie-Hellman
Quantum Diffie-Hellman (QDH), while offering a quantum-resistant key exchange protocol, can be significantly enhanced by integrating Quantum Key Distribution (QKD). QKD provides a fundamentally secure way to establish a shared secret key, addressing the inherent vulnerability of relying solely on computational hardness assumptions, a cornerstone of classical Diffie-Hellman. This integration creates a hybrid approach, leveraging the strengths of both QDH and QKD for superior security.
QKD’s role is to establish a secure channel for transmitting the initial secret key used in the subsequent encryption and decryption processes. Instead of relying on the computational difficulty of solving mathematical problems, QKD uses the principles of quantum mechanics to ensure that any eavesdropping attempt is detectable. This means the shared secret key generated through QDH is then used in conjunction with a perfectly secure key distributed via QKD, enhancing the overall security of the communication.
QKD Protocols in Quantum Diffie-Hellman
Several QKD protocols can be integrated with QDH to enhance its security. The choice depends on factors such as the distance between communicating parties, the required key rate, and the available technology. For example, BB84 (Bennett-Brassard 1984) is a widely known protocol that leverages the properties of polarized photons to transmit information securely. Another protocol, E91 (Ekert 1991), uses entangled photon pairs to generate a shared secret key, offering inherent security through the violation of Bell’s inequalities. These protocols can be used to distribute a secret key that is then used to encrypt the data exchanged using the key established through the QDH protocol. The integration might involve using the QKD key to encrypt the parameters exchanged in the QDH process or using the QKD key as a seed for generating additional keys for longer communication sessions.
Advantages and Disadvantages of Using QKD with Quantum Diffie-Hellman
The decision to integrate QKD with QDH involves weighing several factors. A careful consideration of the advantages and disadvantages is crucial for optimal security and practicality.
The advantages of integrating QKD with QDH are substantial. Firstly, it provides an unprecedented level of security, mitigating the risk of attacks that exploit weaknesses in the computational hardness assumptions of QDH alone. Secondly, the integration offers a robust defense against future advances in quantum computing, ensuring long-term security. Finally, the use of QKD adds a layer of provable security, providing stronger guarantees compared to relying solely on QDH.
- Unprecedented security: QKD eliminates the risk of undetected eavesdropping inherent in purely computational security.
- Future-proof security: Resistant to attacks from both classical and quantum computers.
- Provable security: Offers stronger security guarantees compared to QDH alone.
However, integrating QKD also presents challenges. The main disadvantage is the practical limitations of current QKD technologies. The distance over which QKD can securely transmit keys is limited, and the key generation rate can be relatively low compared to classical methods. Furthermore, QKD systems are complex and expensive to implement, requiring specialized equipment and expertise. Finally, the security of QKD relies on accurate characterization and control of the quantum channel, introducing potential vulnerabilities if not implemented correctly.
- Limited range and key rate: Current QKD technology faces limitations in transmission distance and key generation speed.
- High cost and complexity: QKD systems require specialized equipment and expertise, making them expensive to deploy and maintain.
- Implementation challenges: Accurate characterization and control of the quantum channel are critical for security.
Quantum Algorithms and their Application
Source: slideplayer.com
Quantum Diffie-Hellman, unlike its classical counterpart, relies on the power of quantum computation to achieve secure key exchange. This enhanced security stems from the unique properties of quantum mechanics and the algorithms that exploit them. While classical Diffie-Hellman hinges on the computational difficulty of certain mathematical problems, the quantum version takes advantage of quantum phenomena to offer potentially unbreakable encryption.
The core of Quantum Diffie-Hellman lies in its utilization of quantum algorithms to perform the necessary computations. These algorithms aren’t simply faster versions of classical algorithms; they fundamentally leverage quantum superposition and entanglement to achieve computational feats impossible for classical computers. This shift in computational paradigm significantly enhances the security of the key exchange process.
Quantum Algorithms Used in Quantum Diffie-Hellman
Quantum Diffie-Hellman leverages Shor’s algorithm indirectly, primarily for its role in breaking the underlying cryptography of classical Diffie-Hellman. While not directly used in the key exchange protocol itself, Shor’s algorithm highlights the vulnerability of classical systems and underscores the need for a quantum-resistant alternative. The actual key exchange process in the quantum variant often relies on quantum communication protocols and techniques which are still under development, and there isn’t a single universally adopted algorithm yet. The security of Quantum Diffie-Hellman depends on the assumed hardness of certain quantum computational problems, which are still areas of active research.
Leveraging Quantum Phenomena for Enhanced Security
Quantum mechanics introduces concepts like superposition and entanglement that classical computers cannot replicate. Superposition allows a qubit to exist in multiple states simultaneously, enabling parallel computations. Entanglement links two or more qubits, so that measuring the state of one instantly reveals the state of the others, regardless of the distance separating them. These phenomena allow for quantum algorithms that can solve certain problems exponentially faster than classical algorithms. This speed advantage is crucial in ensuring the security of the quantum key exchange, making it computationally infeasible for an eavesdropper to intercept and decipher the key. For example, the difficulty of solving the discrete logarithm problem, a cornerstone of classical Diffie-Hellman’s security, is drastically altered in the quantum realm, leading to a more robust key exchange.
Simplified Flowchart of Quantum Diffie-Hellman Key Exchange
A simplified flowchart would visually represent the steps. Imagine two parties, Alice and Bob, wanting to establish a shared secret key. The process, while complex at a quantum level, can be conceptually represented as follows:
A simplified flowchart depicting the exchange would show:
1. Alice and Bob agree on a set of quantum parameters: This includes the choice of a suitable quantum algorithm and the communication channel. This is analogous to choosing a prime number and a generator in classical Diffie-Hellman.
2. Alice prepares a quantum state and sends it to Bob: This state is carefully constructed based on the chosen parameters and contains information that will contribute to the shared secret key. This step leverages quantum superposition and potentially entanglement.
3. Bob performs a quantum measurement on the received state and sends a modified state back to Alice: Bob’s actions modify the quantum state, introducing his contribution to the shared secret.
4. Alice performs a measurement on the state received from Bob, extracting the shared secret key: The final measurement by Alice reveals the shared secret key, known only to Alice and Bob due to the nature of quantum mechanics. Any attempt by an eavesdropper to intercept and measure the quantum states would irrevocably alter them, alerting Alice and Bob to the intrusion.
Security Analysis of Quantum Diffie-Hellman
Source: github.io
Quantum Diffie-Hellman (QDH), while offering a seemingly secure key exchange protocol in the quantum realm, isn’t impervious to attacks. Understanding its vulnerabilities is crucial for ensuring its practical implementation and safeguarding sensitive information. This section delves into the potential weaknesses of QDH and explores strategies to mitigate them.
Quantum Diffie-Hellman, like its classical counterpart, relies on the computational difficulty of certain mathematical problems. However, the quantum computing landscape introduces new challenges and vulnerabilities that require careful consideration. While resistant to many classical attacks, QDH faces unique threats stemming from the power of quantum algorithms. The comparison between its resilience against classical and quantum attacks highlights the critical need for robust security measures.
Vulnerabilities of Quantum Diffie-Hellman
Several factors can compromise the security of a QDH key exchange. These vulnerabilities range from flaws in the underlying mathematical assumptions to implementation-specific weaknesses. For instance, the choice of the underlying mathematical group and the size of the parameters significantly influence the protocol’s security. Insufficiently large parameters can make the system susceptible to brute-force attacks, even with quantum computers. Furthermore, side-channel attacks, which exploit information leaked during the computation process (e.g., timing or power consumption), can reveal secret information, jeopardizing the entire key exchange. Finally, imperfect quantum devices, susceptible to noise and errors, could introduce vulnerabilities that a sophisticated attacker could exploit.
Resilience Against Classical and Quantum Attacks
Compared to classical Diffie-Hellman, QDH offers enhanced resistance against classical attacks, primarily because the computational hardness of the underlying problems remains significant for classical computers. However, Shor’s algorithm, a pivotal quantum algorithm, poses a significant threat. Shor’s algorithm can efficiently solve the discrete logarithm problem and the integer factorization problem, both crucial to the security of classical and quantum Diffie-Hellman. This means that a sufficiently powerful quantum computer could potentially break QDH, rendering the exchanged key vulnerable. Therefore, while QDH provides a stronger defense against classical attacks than its classical counterpart, its resilience against future quantum attacks remains a critical concern.
Mitigation Strategies for Quantum Diffie-Hellman Vulnerabilities
Addressing the potential vulnerabilities of QDH requires a multi-faceted approach. Implementing the following strategies can significantly enhance its security:
- Employing Post-Quantum Cryptography: Integrating post-quantum cryptographic techniques alongside QDH can offer a layered security approach. Post-quantum cryptography focuses on algorithms believed to be secure even against quantum attacks. Combining these with QDH provides resilience against both classical and quantum threats. For example, lattice-based cryptography can be used to supplement the QDH exchange, providing an additional layer of protection.
- Parameter Selection: Choosing appropriately large parameters for the underlying mathematical group is crucial. The size of these parameters should be determined based on the expected computational power of future quantum computers, ensuring that even a powerful quantum computer would require an infeasible amount of time to break the system. This requires ongoing research and adaptation to the advancement of quantum computing technology.
- Secure Implementation: Implementing QDH in a way that minimizes side-channel attacks is vital. This involves careful consideration of the hardware and software used, employing techniques like constant-time algorithms and secure memory management to prevent information leakage. Regular security audits and penetration testing can help identify and address any potential vulnerabilities in the implementation.
- Quantum Random Number Generators: Using high-quality quantum random number generators (QRNGs) to generate the ephemeral keys in QDH is crucial. This ensures that the keys are truly random and unpredictable, making it harder for attackers to guess or derive them. QRNGs leverage the inherent randomness of quantum phenomena to generate high-entropy random numbers.
Practical Implementations and Challenges
Quantum Diffie-Hellman (QDH), while theoretically promising, faces significant hurdles in its practical implementation. Its potential, however, is undeniable, driving ongoing research and development across various sectors. Understanding both the nascent applications and the substantial technological challenges is crucial for assessing its future impact.
The current state of QDH implementation is characterized by a gap between theoretical potential and practical realization. While not yet widely deployed in commercial systems, several areas show promising explorations and initial implementations. The primary challenge lies in the technological complexities involved in building and scaling quantum computers capable of reliably performing the necessary quantum computations.
Real-World Applications Under Exploration, Quantum diffie hellman key exchange
Several research groups and organizations are actively exploring the use of QDH in secure communication protocols. These explorations are primarily focused on highly secure government and military communications, where the need for unbreakable encryption is paramount. For instance, research initiatives are investigating QDH’s integration into quantum networks, aiming to establish secure connections between quantum computers and quantum sensors. These nascent applications highlight the potential of QDH to secure future quantum-based infrastructure. Further research is also exploring QDH’s integration into hybrid quantum-classical systems, leveraging the strengths of both classical and quantum technologies.
Technological Challenges in Scaling QDH
Implementing QDH at a scale comparable to classical Diffie-Hellman presents formidable technological challenges. The most significant obstacle is the inherent fragility of quantum systems. Quantum bits (qubits), the fundamental units of quantum computation, are extremely susceptible to environmental noise and decoherence, leading to errors in computation. Maintaining the coherence of qubits for the duration of a QDH exchange is a major technological hurdle. Furthermore, building and maintaining large-scale, fault-tolerant quantum computers with sufficient qubit count and coherence time represents a substantial engineering challenge. The development of robust quantum error correction codes is also critical for ensuring reliable QDH implementations. Finally, the cost and complexity of quantum computing hardware remain significant barriers to widespread adoption.
Potential Impact on Various Industries
The successful implementation of QDH could revolutionize several industries. The financial sector, for example, could leverage QDH to secure sensitive financial transactions and protect against quantum-resistant attacks. Healthcare could benefit from enhanced security for electronic health records and patient data. The defense and intelligence sectors could utilize QDH for highly secure communications and data protection. Furthermore, the development of quantum-secure communication networks based on QDH could be transformative for various sectors reliant on secure data transmission, including energy grids and transportation systems. The impact, however, hinges on overcoming the considerable technological challenges and reducing the cost of quantum computing hardware.
Future Directions and Research
Quantum Diffie-Hellman (QDH), while promising, is still an active area of research. Its development hinges on overcoming several hurdles and exploring avenues for improvement to ensure its robustness and widespread adoption in a future quantum-resistant cryptographic landscape. Further advancements will significantly impact secure communication in the quantum era.
The continued development of QDH faces several open questions and challenges that require focused research efforts. These range from enhancing protocol efficiency to exploring novel approaches for achieving higher levels of security and practicality. Addressing these issues will be crucial for realizing the full potential of QDH.
Open Research Questions in Quantum Diffie-Hellman
Several critical aspects of QDH remain open research questions. These questions are not merely theoretical; they directly impact the feasibility and security of implementing QDH in real-world applications. For instance, optimizing the efficiency of the quantum computations involved is paramount for practical deployment. Additionally, ensuring resistance against emerging quantum attacks requires ongoing investigation.
Potential Improvements and Extensions of Quantum Diffie-Hellman Protocols
Several avenues exist for improving current QDH protocols. One significant area focuses on enhancing the efficiency of the underlying quantum algorithms. This could involve exploring alternative quantum algorithms that require fewer quantum resources or developing more efficient implementations of existing algorithms. Another key improvement lies in developing techniques for better managing and mitigating errors inherent in quantum computations. Robust error correction schemes are crucial for ensuring the reliability of QDH in noisy quantum environments. Finally, research into post-quantum cryptography can inform the development of hybrid protocols that combine the strengths of both classical and quantum cryptographic techniques. This hybrid approach could provide a robust and practical solution in the transition period to a fully quantum-secure infrastructure.
Projected Evolution of Quantum Diffie-Hellman Technology
Imagine a graph charting the evolution of QDH over the next decade. The x-axis represents time, spanning from the present to 2034. The y-axis represents several key metrics: protocol efficiency (measured, for example, by the number of quantum gates required), security level (measured by resistance to known quantum attacks), and implementation complexity (measured by the resources required for practical implementation). The graph would initially show a relatively steep upward curve for efficiency and security, reflecting the rapid advancements in quantum computing and cryptography research. This reflects the ongoing development of better quantum algorithms and error correction codes. However, as the technology matures, the curve might flatten somewhat, indicating that further improvements become incrementally more challenging. A similar trend is expected for implementation complexity; initially high due to the nascent nature of the technology, it should gradually decrease as hardware and software mature, making QDH more accessible. By 2034, we might expect to see a plateau representing a level of maturity where QDH is widely implemented in secure communication systems, possibly alongside other post-quantum cryptographic techniques. This mirrors the evolution of RSA encryption, which initially required significant computational power but eventually became ubiquitous thanks to hardware and algorithmic improvements. This scenario, however, assumes continued investment in research and development and successful resolution of the challenges Artikeld above. A less optimistic scenario could see slower progress, potentially hampered by unforeseen obstacles or a lack of sufficient resources.
Final Wrap-Up
So, there you have it – a glimpse into the fascinating world of Quantum Diffie-Hellman Key Exchange. From its theoretical foundations to its practical implications, this technology represents a monumental leap forward in cybersecurity. While challenges remain, the potential to revolutionize secure communication is undeniable. As quantum computing continues to advance, Quantum Diffie-Hellman is poised to become the gold standard for protecting our digital lives. The future of online security is quantum, and it’s more secure than ever before.